Los Números Reales
En matemáticas, los números reales (designados por ℝ) incluyen tanto a los números racionales (positivos, negativos y el cero) como a los números irracionales; y en otro enfoque, trascendentes y algebraicos. Los irracionales y los trascendentes1 (1970) no se pueden expresar mediante una fracción de dos enteros con denominador no nulo; tienen infinitas cifras decimales aperiódicas, tales como: √5, π, el número real log2, cuya trascendencia fue enunciada por Euler en el siglo XVIII.1
Los números reales pueden ser descritos y construidos de varias formas, algunas simples aunque carentes del rigor necesario para los propósitos formales de matemáticas y otras más complejas pero con el rigor necesario para el trabajo matemático formal.
1.- Numeros Racionales
Si se necesita además dividir, surgen los números racionales (o fraccionarios, o quebrados),
|
- Los racionales se obtienen a partir de los enteros añadiendo los inversos para la multiplicación.
De este modo, el conjunto de los racionales, con las operaciones de suma y producto tiene estructura de cuerpo conmutativo.
- La suma de dos racionales a/b y c/d se define como a/b+c/d=(ad+cb)/bd.
- El producto de dos racionales a/b y c/d se define como ac/bd.
- Dos números racionales a/b y c/d son iguales si y sólo si ad=bc.
(En todo lo anterior, a, b, c y d denotan números enteros)- Un número racional se dice que está expresado mediante una fracción irreducible si el numerador y el denominador no tienen factores comunes.
- En
se pueden resolver todas las ecuaciones lineales, es decir, aquéllas de la forma ax+b=0, con a y b racionales.
- En
se puede definir un orden total compatible con las operaciones suma y producto definidas anteriormente y que extienda el orden existente en
y en
. Para ello basta con definirlo como sigue:
Dados dos números racionales a/b y c/d, donde b y c son enteros positivos (esto siempre puede conseguirse, por ejemplo, si b es negativo basta con multiplicar a y b por -1 para obtener un número racional igual que el dado pero con denominador positivo), se dice que
Por tantosi y sólo si
respecto del orden existente en el conjunto de los enteros.
con dicho orden es un conjunto totalmente ordenado.
Densidad del orden:
Dados dos números racionales distintos,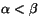 , siempre existe otro número racional
, siempre existe otro número racional 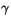 tal que
tal que 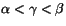 .
.
Dados dos números racionales distintos,
- Para ello, si
Ejercicio: probar que efectivamente
- Por ejemplo, ahora entre 3/5 y 5/8 se encuentra 8/13, entre 3/5 y 8/13 se encuentra 11/18, etc., tenemos asi 3/5 < ...... < 11/18 < 8/13 < 5/8 < 2/3.
Propiedad arquimediana (o de Arquímedes):
Dados dos números racionales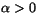 y
y 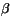 , siempre existe un n natural tal que
, siempre existe un n natural tal que 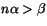 . Esto quiere decir que por pequeño que sea
. Esto quiere decir que por pequeño que sea 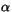 , si consideramos la sucesión de racionales
, si consideramos la sucesión de racionales 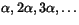 , llegará un momento en que sobrepasasaremos a
, llegará un momento en que sobrepasasaremos a 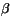 , por muy grande que este sea.
, por muy grande que este sea.
Dados dos números racionales
- Por ejemplo:
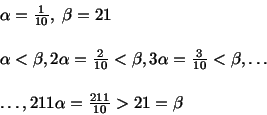
Representación decimal de números racionales:
Todo número racional admite una representación decimal, que es la que se obtiene al dividir el numerador entre el denominador, por ejemplo 1/2 tiene como expresión decimal 0.5 , 3405/25=136.2 y 1/3= 0.33333.......
Todo número racional admite una representación decimal, que es la que se obtiene al dividir el numerador entre el denominador, por ejemplo 1/2 tiene como expresión decimal 0.5 , 3405/25=136.2 y 1/3= 0.33333.......
Esto puede dar lugar a dos tipos de expresiones decimales, las exactas y las periódicas. Éstas últimas pueden a su vez dividirse en periódicas puras o periódicas mixtas.
- Expresión decimal exacta, es aquélla que tiene un número finito de términos. Por ejemplo: 0.5, 1.348 ó 367.2982345
Esta expresiones surgen de números racionales cuyo denominador (en la expresión irreducible) sólo contiene los factores 2 y 5. Por ejemplo 1349/1000, 40/25, ... - Expresión decimal periódica es aquélla que tinene un número infinito de cifra decimales, pero de modo que un grupo finito de ellas se repite infinitamente, de forma periódica, por ejemplo 0.333333....., 125.67777777....... ó 3.2567256725672567......
Surgen de fracciones cuyo denominador contiene factores distintos de 2 y 5, por ejemplo, 1/3=0.33333.....
La parte que no se repite se denomina anteperíodo y la que se repite, período.- Periódica pura es aquélla que no tiene anteperíodo.
- Periódica mixta es aquélla que sí tiene anteperíodo.


No hay comentarios.:
Publicar un comentario