Números Irracionales
El concepto de números irracionales proviene de la Escuela Pitagórica, que descubrió la existencia de números irracionales, es decir que no eran enteros ni racionales como fracciones. Esta escuela, los llamó en primer lugar números inconmensurables.
Definición:
Los números irracionales tienen como definición que son números que poseen infinitas cifras decimales no periódicas, que por lo tanto no pueden ser expresados como fracciones.
Estos números pueden haber sido descubiertos al tratar de resolver la longitud de un cuadrado según el Teorema de Pitágoras, siendo el resultado el número
la raíz de 2 es 1.4142135623730950488016887242097, el ejemplo de números irracionales más claro e inmediato, cuya respuesta a su vez posee infinitas cifras decimales que al no poder ser fraccionado, fue llamado irracional, en el sentido de no poder escribirlo como una ración o varias raciones o fracciones.
Números irracionales famosos:
 |
Pi es un número irracional famoso. Se han calculado más de un millón de cifras decimales y sigue sin repetirse. Los primeros son estos:
3,1415926535897932384626433832795 (y sigue...)
| ||||
 |
El número e (el número de Euler) es otro número irracional famoso. Se han calculado muchas cifras decimales de e sin encontrar ningún patrón. Los primeros decimales son:
2,7182818284590452353602874713527 (y sigue...)
| ||||
 |
La razón de oro es un número irracional. Sus primeros dígitos son:
1,61803398874989484820... (y más...)
| ||||
 |
Muchas raíces cuadradas, cúbicas, etc. también son irracionales. Ejemplos:
Pero √4 = 2, y √9 = 3, así que no todas las raíces son irracionales. |
Historia de los números irracionales:
Aparentemente Hipaso (un estudiante de Pitágoras) descubrió los números irracionales intentando escribir la raíz de 2 en forma de fracción (se cree que usando geometría). Pero en su lugar demostró que no se puede escribir como fracción, así que es irracional.
Pero Pitágoras no podía aceptar que existieran números irracionales, porque creía que todos los números tienen valores perfectos. Como no pudo demostrar que los "números irracionales" de Hipaso no existían, ¡tiraron a Hipaso por la borda y se ahogó!.
Pero Pitágoras no podía aceptar que existieran números irracionales, porque creía que todos los números tienen valores perfectos. Como no pudo demostrar que los "números irracionales" de Hipaso no existían, ¡tiraron a Hipaso por la borda y se ahogó!.
Euclides (300 a.C.) recoge en su obra Los Elementos una referencia a los números irracionales y prueba el siguiente teorema que, posiblemente ya fue probado casi 300 años antes por el propio Pitágoras o alguno de sus discípulos.
EL NUMERO π:
Pi
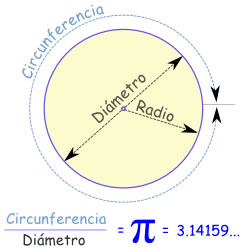
La proporción entre la circunferencia y
el diámetro de un círculo.
Es aproximadamente:
3,14159265358979323846…
Las cifras siguen y siguen sin un patrón. De hecho aunque calcules un millón de cifras decimales no encontrarás que se repiten.
|  |
Aproximación:
Una aproximación rápida y fácil de pi es 22/7
22/7 = 3,1428571...
Pero como ves, 22/7 no es el valor exacto. De hecho pi no es igual a ninguna fracción, por eso es un número irracional.
EL NUMERO e:
 |
El número e es un número irracional famoso, y es uno de los números más importantes en matemáticas.
Las primeras cifras son:
2,7182818284590452353602874713527 (y sigue...)
Se lo suele llamar el número de Euler por Leonhard Euler
e es la base de los logaritmos naturales (inventados por John Napier). Por otra parte los logaritmos comunes tienen base 10.
|
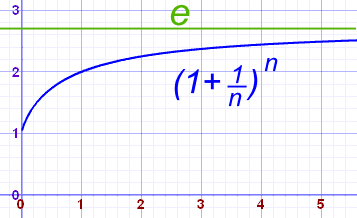
Calcularlo
El valor de (1 + 1/n)n se aproxima a e cuanto más grande es n:
|  |
OTROS IRRACIONALES:
Ejemplos de números irracionales:
En primer lugar vamos a anotar los ya mencionados números irracionales algebraicos con ejemplos, ya habíamos hablado de √2 o raíz cuadrada de dos que resulta de una ecuación algebraica, pero también tenemos otros ejemplos que podrían resultar son:
y
Por otro lado, tenemos a los números irracionales trascendentes, que no pueden representarse mediante radicales como se lo ha hecho en el ejemplo anterior, sino que deben ser representados con decimales infinitos no periódicos, y con tres puntos suspensivos para denotar que son infinitos, de lo contrario estaríamos escribiendo números durante toda la eternidad, así:
0,1961325454898161376813268743781937693498749…
0,01001000100001000001000000100000001000000001…
0,01001000100001000001000000100000001000000001…
Aquí un vídeo sobre los números irracionales:
No hay comentarios.:
Publicar un comentario