Anillo de los numeros enteros

ANILLO DE LOS NUMEROS

El anillo de todos los enteros (positivos, negativos o cero), usualmente indicado como Z.

Dado un campo numérico algebraico K, los enteros algebraicos contenidos en K forman un anillo, el anillo de los enteros de K, comúnmente indicado como O_Ku .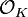

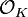Usando esta notación, se puede escribir Z = O_Q dado que Z es el anillo de enteros del campo Q de números racionales. Y en efecto por esta razón, en la teoría algebraica de números los elementos de Z son comúnmente llamados los "enteros racionales".

El anillo de los números enteros O_K tiene una base integral; lo que significa que existe b₁,...,b_n ∈ O_K (la base integral) tal que cada elemento x en O_K puede ser unívocamente representado como

con a_i ∈ Z

Propiedades de la adición en Z

En el conjunto de los números enteros se cumplen todas las propiedades que tú ya conoces para la adición. Estas son: clausura, conmutatividad, asociatividad y elemento neutro.

En ejemplos:

1) Clausura: toda adición tiene resultado.
-2 + -8 = -10

2) Conmutativa: el orden de los sumandos no cambia la suma.
-6 + +2 = +2 + -6

3) Asociativa: sólo podemos sumar 2 números a la vez, y lo representamos con paréntesis.
(-3 + +4) + -2 = -3 + (+4 + -2)

4) Elemento neutro: cualquier entero sumado con 0 tiene como suma a dicho entero.
+8 + 0 = +8 

5) Elemento inverso aditivo: en la adición de enteros aparece esta nueva propiedad. Se llama así al número que, sumado con otro, nos da como suma el elemento neutro.
En otras palabras, será sumar 2 números enteros cuya suma nos dé 0.

¿Cuáles serán los números que cumplan esa condición?

Sumemos:

+6 + -6 = 0
-18 + +18 = 0

Quiere decir que llamamos elemento inverso aditivo al opuesto de un número entero.

Entonces, el inverso aditivo de -327 es +327 y el inverso aditivo de +4 es -4, etcétera.