COMBINACIÓN LINEAL
Una combinación lineal es una expresión matemática que consiste en la suma entre pares de elementos, de determinados conjuntos, multiplicados entre sí.
En particular, la combinación lineal de un conjunto de vectores se trata de un vector de la forma
con los 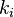 elementos de un cuerpo.
elementos de un cuerpo.
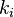 elementos de un cuerpo.
elementos de un cuerpo.
Definición:
Dados dos conjuntos cualesquiera A y B.
|
Resulta de especial interés la definición de combinación lineal de un vector con respecto a un conjunto.
Espacios vectoriales
Dado un espacio vectorial V sobre un cuerpo  y un conjunto
y un conjunto  de vectores en V, es decir,
de vectores en V, es decir,  .
.
 y un conjunto
y un conjunto  de vectores en V, es decir,
de vectores en V, es decir,  .
.
|
En términos no tan formales, diremos que  es combinación lineal de vectores de
es combinación lineal de vectores de  si podemos expresarlo como una suma de productos por escalar de una cantidad finita de elementos de
si podemos expresarlo como una suma de productos por escalar de una cantidad finita de elementos de  . En este caso, también se dice que
. En este caso, también se dice que  depende linealmente de los vectores de
depende linealmente de los vectores de  .
.
 es combinación lineal de vectores de
es combinación lineal de vectores de  si podemos expresarlo como una suma de productos por escalar de una cantidad finita de elementos de
si podemos expresarlo como una suma de productos por escalar de una cantidad finita de elementos de  . En este caso, también se dice que
. En este caso, también se dice que  depende linealmente de los vectores de
depende linealmente de los vectores de  .
.
Ejemplos.
Ejemplo 1. Considere el espacio vectorial R3 de triadas ordenadas de números reales, sobre el campo
de los números reales R, con las operaciones usuales de adición y multiplicación por un escalar real.
1. Considere el conjunto S = {~v1}, formado por un único vector ~v1. Entonces, el espacio [S] esta dado
por
[S] = {λ~v1|λ ∈ K}
Geometricamente [S] esta formado por una línea que pasa por el origen y tiene la dirección del
vector ~v1.
2. Considere el conjunto S = {~v1,~v2}, formado por dos vectores ~v1,~v2. Entonces, el espacio [S] esta dado
por
[S] = {λ1~v1 + λ2~v2|λ1,λ2 ∈ K}
Geometricamente [S] esta formado por un plano que pasa por el origen y contiene a los vectores ~v1
y ~v2. Mas aun, una normal al plano esta dada por ~v1 × ~v2, donde × indica el producto vectorial de
los vectores.
A CONTINUACIÓN UN VÍDEO CON UNA BREVE EXPLICACIÓN:


 es combinación lineal de A si
es combinación lineal de A si  .
.
No hay comentarios.:
Publicar un comentario